Algunos cálculos para el inversionista
Hoy tengo una publicación más corta, con algunos conceptos matemáticos que nos pueden ayudar a pensar de forma más efectiva sobre nuestras inversiones.
En el pasado he aludido a algunos de estos, y me pareció una buena idea tener todo en un mismo lugar.
1. El ahorro y el retorno
Una inquietud común de la gente que empieza a invertir es: ¿dónde encuentro la mejor inversión, con el retorno más alto? La idea atrás de esto es que invertir es un juego de conocimiento, donde saber cuál es la mejor opción es tener casi todo el juego ganado.
Y bueno, no hay nada fundamentalmente malo en la búsqueda de la inversión más rentable. Sobre todo si entendemos correctamente los riesgos a los que nos estaríamos exponiendo y sabemos por qué es que esta inversión nos paga más que sus alternativas. Pero esta búsqueda puede ser lenta, difícil, llena de complejidades… Puede consumir mucha energía, que talvez aprovecharíamos mejor de otras formas.
La realidad de invertir es que es una actividad en la que hay muchos factores que aportan al éxito de largo plazo. El retorno de las inversiones es uno, pero hay otro que no recibe tanta atención y es aún más importante en las etapas tempranas de construcción de un capital. Ese factor es el ahorro: cuánto estamos aportando o invirtiendo.
Tener una buena disciplina de ahorro puede tener un mayor impacto en nuestros resultados que aumentar el retorno de las inversiones.
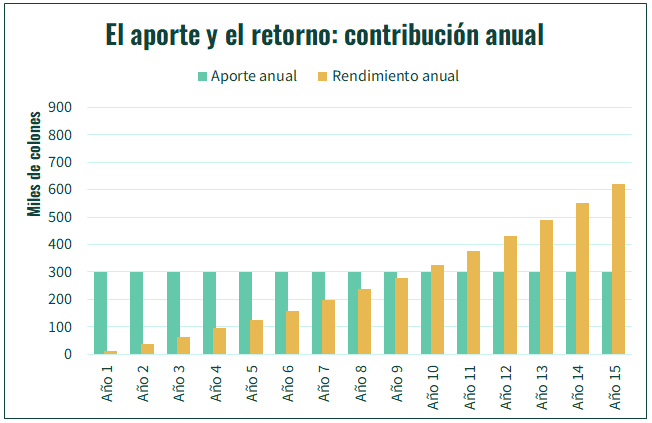
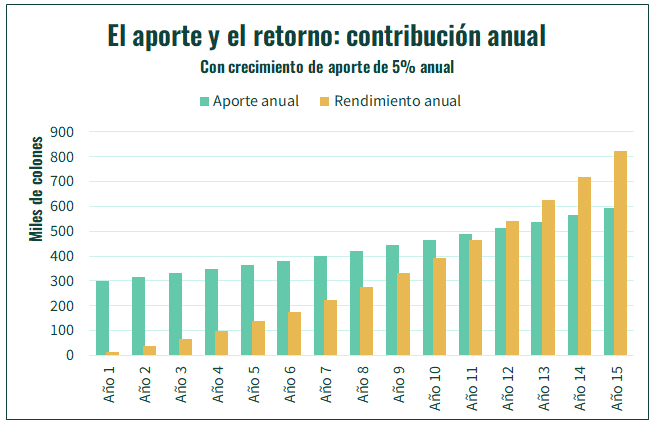
Les presento el siguiente ejemplo. Hay un inversionista que ahorra ₡25 000 cada mes, ₡300 000 en un año. El inversionista recibe, sobre el monto ahorrado, un 8% de retorno. Vamos a ver los primeros 15 años de ahorro.
Durante los primeros años, el capital de inversionista crece, principalmente, por el aporte. Por ejemplo, el primer año, el capital crece ₡310 000 colones; ₡300 000 por aportes y ₡10 000 por retornos. Estos ₡10 000 difícilmente cubran el costo del tiempo invertido en buscar mejores opciones de inversión.
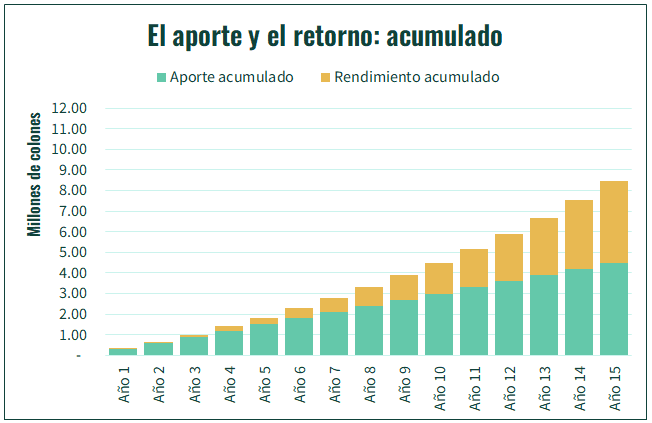
Es hasta ya pasado el tiempo, cerca de 10 años después de empezar a ahorrar, que el impacto del rendimiento empieza a ser igual o más importante que el impacto del aporte periódico. Podemos verlo en los siguientes gráficos.
Acá alguno podrá pensar: “Sí, muy bonito todo esto, pero si el retorno fuera más alto, habría un crecimiento más rápido, ¿no?”
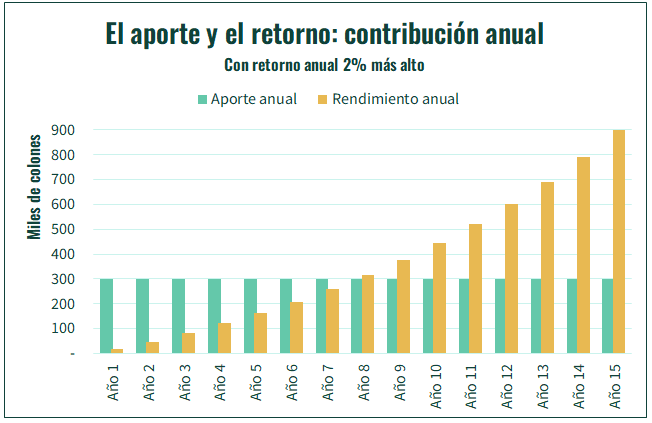
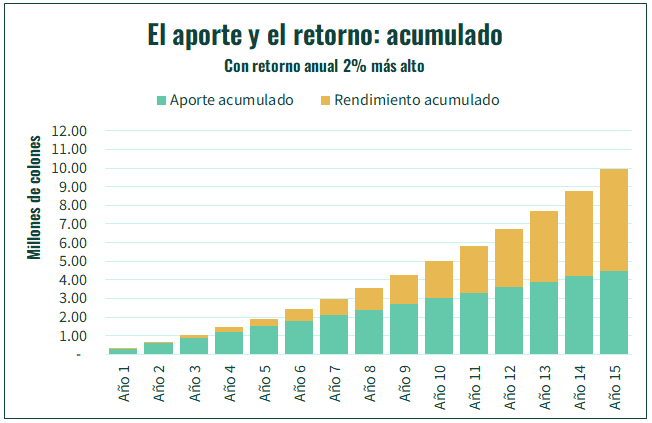
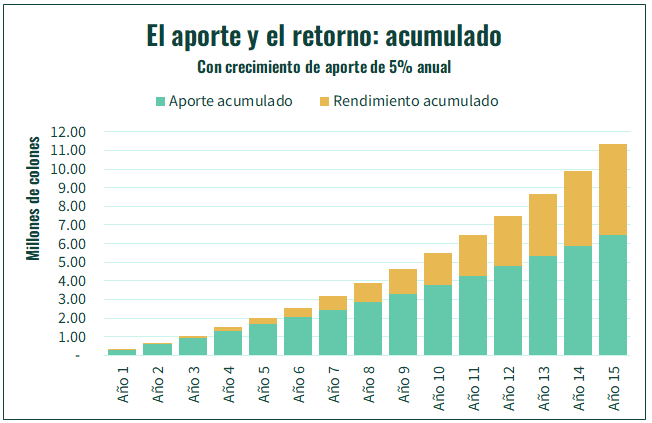
Y sí, con un retorno más alto, de 10%, vemos un crecimiento más acelerado de los montos, tanto del de rendimiento anual, como del acumulado. Con un rendimiento de 10% alcanzamos casi ₡10 millones luego de 15 años, contra los ₡8.5 millones a los que se llega con un 8% de rendimiento.
Pero esta no es toda la historia. ¿Qué pasaría en cambio si nos mantenemos con el retorno de 8%, pero aumentamos en un 5% nuestro aporte todos los años? En este caso, vemos un crecimiento aún más rápido de los acumulados, que al cabo de 15 años llegan a un nivel de ₡11.3 millones.
En general, durante los primeros años de nuestro ahorro, la intervención más importante que podemos hacer para mejorar nuestros resultados es aumentar nuestra tasa de ahorro. Cualquier energía adicional estará mejor invertida en afectar esta variable que en encontrar un instrumento de inversión mágico que nos dé más retorno con menos riesgo.
Ojo que esto no quiere decir que SIEMPRE va a importar más la tasa de ahorro que el retorno de nuestras inversiones, pero el punto en el que nos va a importar más el retorno de nuestras inversiones viene adelante, cuando tengamos un monto acumulado significativo, ojalá de entre ₡50 y ₡100 millones. Por esta razón en publicaciones como Independencia financiera en una página y El mejor portafolio de inversión para la mayoría de los costarricenses recomiendo utilizar estrategias de inversión diversificadas, simples y fáciles de implementar, sobre hacer apuestas especulativas en inversiones de alto rendimiento, sobre todo cuando uno no cuenta con un saldo importante.
2. 200 a 1
La regla de 200 a 1 se basa en la matemática de una anualidad (annuity en inglés). La anualidad es una forma de convertir pagos periódicos, con una tasa de interés, en un monto único.
La fórmula para calcular el valor presente (VP) de una anualidad ordinaria es:
Donde:
C es el pago periódico (anualidad).
r es la tasa de interés por período.
n es el número total de pagos.
Esta fórmula nos permite convertir un monto pagadero hoy (VP) en una serie de pagos pequeños e iguales a lo largo del tiempo (C), considerando el número de pagos (n) y la tasa de interés (r).
Este cálculo nos sirve para estimar los pagos de un crédito o hipoteca, al comparar lo que se recibe hoy con lo que se debe pagar cada mes. Pero, más significativamente para nuestros propósitos, nos ayuda a saber cuánto podríamos recibir cada mes, si tenemos un saldo importante acumulado y nos pagan una rentabilidad r.
Supongamos entonces que queremos saber cuál es la riqueza que debemos tener al retiro para recibir una unidad de salario (que contabilizaremos como un 1) por los 35 años posteriores al momento de la pensión.
En este ejemplo:
C es el pago periódico mensual, igual a 1.
r es el retorno de las inversiones, que suponemos será 5% real anual, 5%/12 cada mes.
n es el número total de pagos, de 12 meses por 35 años, igual a 420 meses.
Introduciendo estas variables en la fórmula tenemos:
Así, podemos ver que con el retorno real de 5%, necesitamos tener cerca de 200 veces el pago mensual que deseamos, para recibir ese pago por 35 años.
Esta regla de 200 a 1 la he usado en publicaciones como Un vistazo al ahorro de pensión complementaria en Costa Rica o Finanzas después de la muerte para explicar el uso de sumas grandes para mantener el estilo de vida en el tiempo.
3. Algunas relaciones rápidas
En el mundo de las inversiones hay algunas relaciones numéricas que se pueden usar como aproximaciones para hacer cálculos mentales y tomar decisiones rápidas. Algunas de las más importantes son:
A. Regla de 72: Sirve para calcular el número de años que toma duplicar un monto invertido a partir de un porcentaje de retorno. Para encontrar el número de años se divide 72 entre el retorno. Así, una inversión que paga 8% tardará 9 años (72/8) en duplicarse, y una inversión que paga 10% tardará poco más de 7 años (72/10) en duplicarse.
Estos números son aproximados, pero dan una idea de los plazos de duplicación.
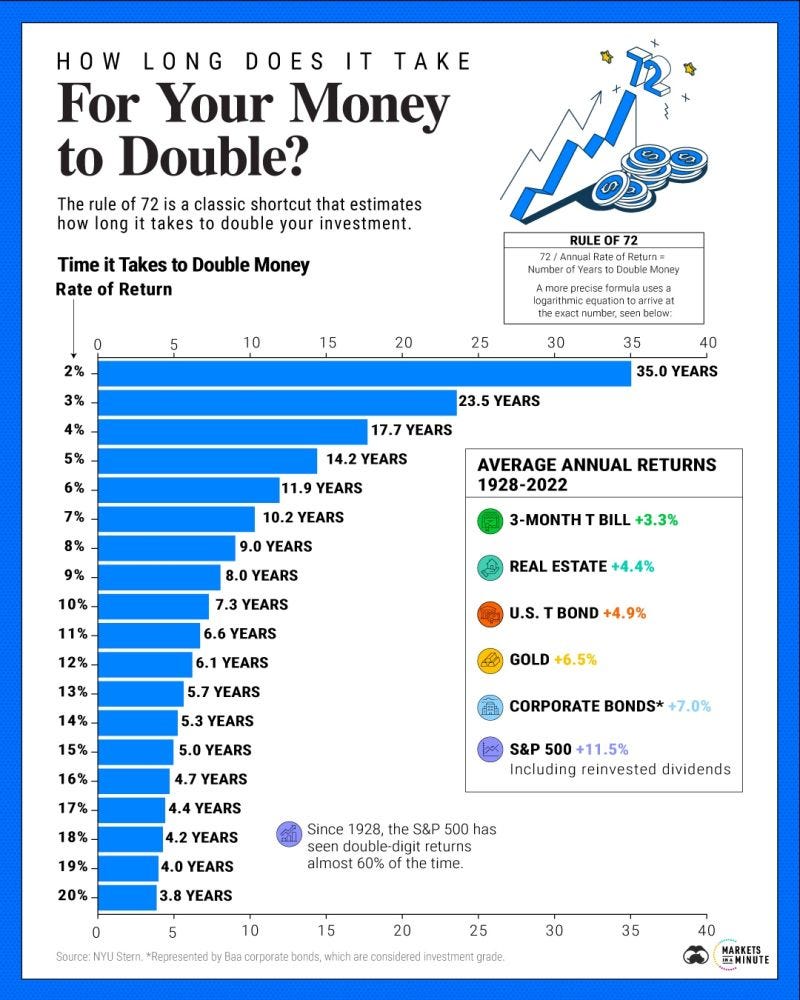
También, podemos hacer ajustes para saber cuándo se triplicaría el monto, usando una “regla” de 114, o cuándo se cuadruplicaría el monto, con una “regla” de 144.
B. Regla de 70: Sirve para calcular el plazo en el que el poder de compra se reduce a la mitad, dada una tasa de inflación. Sólo se divide 70 entre la tasa de inflación.
Así, por ejemplo, con una tasa de inflación de 10%, el dinero pierde la mitad de su poder de compra en 7 años (70/10), y con una tasa de inflación de 3%, que es la meta del BCCR, el dinero pierde la mitad de su poder de compra en poco más de 23 años.
Espero que todo esto les sea de utilidad. Si tienen alguna sugerencia o duda, aprovechen los comentarios. Y si no lo han hecho, suscríbanse para seguir recibiendo La Ruta en su correo electrónico.